Решенија
Ниво 1
Дали добивте 12? Или можеби 1? Не, ова не е во ред.
Точен одговор е: 30. Факт е дека на крајот на првиот и вториот ред нема знак после последната „1“. Тогаш излегува дека цифрите на крајот на првиот ред и на почетокот на вториот се споени, но бидејќи немало место отишле на нов ред. Значи во задачата има две 11-ки.
Ниво 2
Бидејќи целосно езерото ќе биде обраснато за 42 дена и секој ден лилјаните се зголемуваат 2 пати, на 41-виот ден ќе биде обраснато точно половина, а потоа ќе се зголеми два пати.
Ниво 3
Да, ќе може да го спаси сиромашното момче.
Временскиот интервал меѓу 1 и 6-тиот куршум е 5 секунди, односно збирот на интервалите меѓу куршумите е 5. Такви интервали има 5 (1-2, 2-3, 3-4, 4-5, 5-6), бидејќи првиот куршум го пука во 0 секунда, а 6-тиот во 5-тата. Значи времето меѓу два куршуми е 1 секунда. Ако првиот куршум го испука во 0 секунда, вториот ќе го испука во 1, а третиот точно на 2 секунда.
Ниво 4
Се претпоставува дека двата воза се движат со постојана брзина, а шините се паралелни и имаат иста должина. Исто така е познато дека тие истовремено почнуваат да се движат.
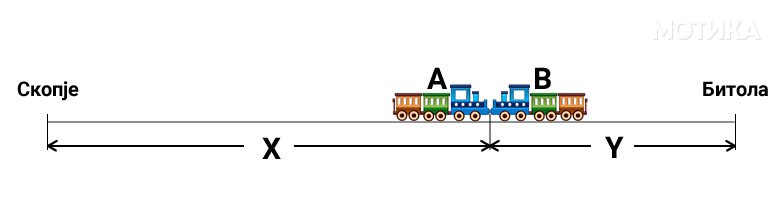
Возот А за 1 час го поминува растојанието Y.
Возот B за 4 часa го поминува растојанието X.
Така, брзината на возот А (изминат пат во единица време е) е V1=Y/1, а брзината на возот B е V2=X / 4.
Бидејќи за до сега поминатиот пат не го знаеме времето, ќе го означиме со t. За брзината на првиот воз имаме V1=X/t, а за вториот V1=Y/t.
Ако вредностите на V1 i V2 од доле ги замениме во горните равенства, ќе добиеме
X/t = Y/1
Y/t = X/4
Сега да го изразиме t од едната равенка и да го замениме во другата ќе го добиеме соодносот на X и Y
Од втората равенка следува дека t=4Y/X, па заменето во првата ни дава дека X=2Y.
По ова, можеме да кажеме дека ако брзината на возот A е Y, брзината на возот B треба да биде (2Y / 4) = Y / 2.
Ова значи дека возот A е 2 пати побрз од возот B. И тие се сретнале 2 часа по почетокот, кога возот А веќе преминал 2/3 од патот, додека возот Б поминал само 1/3 од патот.
Ниво 5
Одговор: 15 м.
Ѕидот, подот и скалата формираат правоаголен триаголник. Скалите се хипотенуза, а ѕидот и подот се катетите. За правоаголни триаголници, се применува Питагорова теорема која вели дека квадратот над хипотенузата е еднаков на збирот на квадратите над катетите. За скала долга 25 метри, нејзиниот квадрат е 625 квадратни метри.
И квадратот од една од катетите е 49 квадратни метри. Ова значи дека квадратот над катетата која го претставува ѕидот е 625 – 49 = 576 квадратни метри.
Значи, горниот дел на скалата на почетокот бил поставен на висина еднаква на √576 = 24 m.
Ако скалата се лизга по ѕидот за 4 м, висината се намалува на 20 м. Сега квадратот на катетата на ѕидот е 400 м, така што квадратот на подножјето е 225 квадратни метри. Ова ни го дава новото расојание од ѕидот до долниот дел од скалата: √225 = 15 m.


