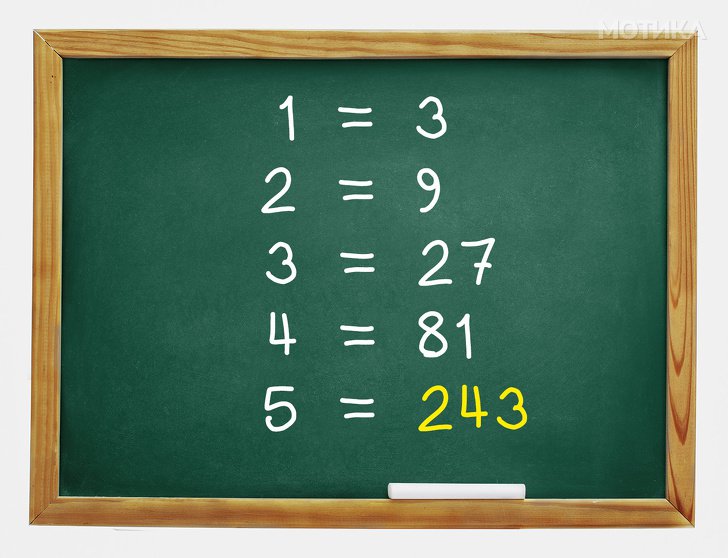Решенија:
1. Цифрите на левата страна се всушност степените на борјот 3. Значи наместо прашалникот треба да стои вредноста на 3 на степен 5, односно 243.
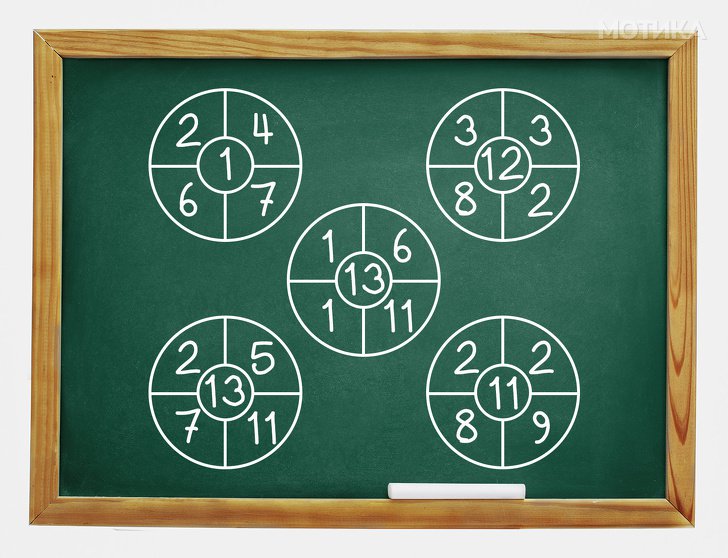
2. Треба да се гледаат сите кригови заедно а не еден по еден. Збирот на броевите што се лево горе на круговите е 10, зборот на сите броеви што се десно горе на круговите е 20, збирот на броевите од лево доле на круговите е 30, што значи десно би бил 40 а во средина 50.
3. Вкупниот циклус на вклучување и исклучување на 1, 2 и 3 светилник трае 2, 4 и 6 секунди, соодветно. Затоа, за да откриете на колку секунди сите три светилници ќе светнат во исто време, треба да го најдете најмалиот заеднички содржател од 2, 4 и 6, кој е еднаков на 12.
4. Ако правоаголникот има средна линија, тогаш бројот на редови ќе биде непарен. Бидејќи има само 20 квадратчиња, имаме само една опција: правоаголникот се состои од 5 линии со по 4 квадратчиња во секоја од нив. Како резултат на тоа, Јован избоил 4 квадратчиња, а 16 останале неизбоени.
5. Овој проблем треба да се реши од крајот. Ние знаеме дека Маша има 9 бонбони откако му дала половина на Сашо; тоа значи дека пред тоа имала 18. Бидејќи Сашо завршил со 17 бонбони, затоа претходно имал 8. Тоа значи дека добил двојно повеќе бонбони од неговата мајка, односно 16. Со оглед на тоа дека вкупниот број на бонбони е 17 + 9 = 26, тогаш Маша му дала 26 – 16 = 10 бонбони на Сашо.